What happens if you apply the function f(z,c) itself as Z-Transformation to the function f(z,c), or even more than once?
I.e. you do f(f(z,c),c), defined here as f2, or f(f(f(z,c),c),c), defined here as f3.
It seems the fractal set is idempotent in respect to Z-Transformations with its generation function f(z,c).
In this case idempotent means: the form of the fractal set does not change.
But as you can see in the examples below the oscillation properties of the heads are changing:
- f(f) == f2: head with former oscillation number 2 is now a fixed point head
- f(f(f)) == f3: head with former oscillation number 3 is now a fixed point head
- f(f(f(f)))) == f4: heads with former oscillation number 2 and 4 are now fixed point heads
- f6: heads with former oscillation number 2,3 and 6 are now fixed point heads
- f12: heads with former oscillation number 2,3,4,6 and 12 are now fixed point heads
This results in a subsequence of the original sequence.
If the original sequence oscillates with a period of 2 or 3 or 6 the subsequence is a fixed point sequence.
E.g.: 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 ---> 3 3 3 3 3 3 3 3
In the following examples Tierazon2 renders fixed point sequences with a brown coloring.
The mathematical rendering renders fixed point sequences with color blue.
| Example | f | f2 | f3 | f4 | f6 | f12 |
| Mandelbrot set rendered with Tierazon2 |

|

|

|

|

|

|
| Mandelbrot set rendered mathematically |
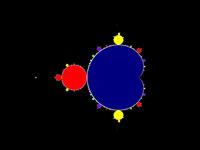
|
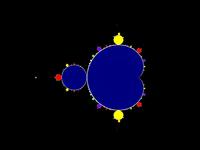
|

|

|
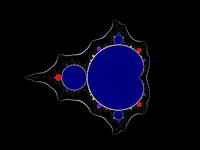
|
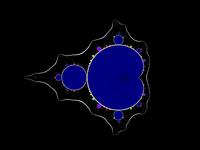
|
| z*atan(z) rendered with Tierazon2 |

|

|

|

|

|

|
| z*atan(z) rendered mathematically |
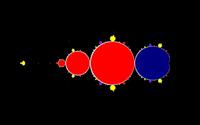
|

|
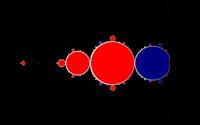
|
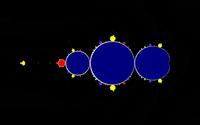
|

|
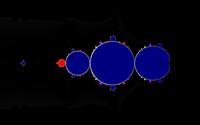
|
