The sequence of numbers z0, z1, z2,.. for the classical apple manikin: z2+c
In a fractal image to every pixel is assigned a sequence of numbers.This sequence of numbers can be:
Every pixel in the image is assigned a color, depending on this sequence of numbers. For the mathematical rendering the colors chosen are:
- The brightness of each color is the average of the sequence |z0|, |z1|, |z2|,..
- color grey: divergence
- color cyan: speed of divergence, bright cyan: slow divergence
- color blue: fixpoint convergence z = f(z), bright blue: slow convergence
- color red: oscillation divergence with number of oscillation points: 2,4,8,16,32,64
- color yellow: oscillation divergence with number of oscillation points: 3,6,12,24,48,96
- color purple: oscillation divergence with number of oscillations points: 5,10,20,40,80
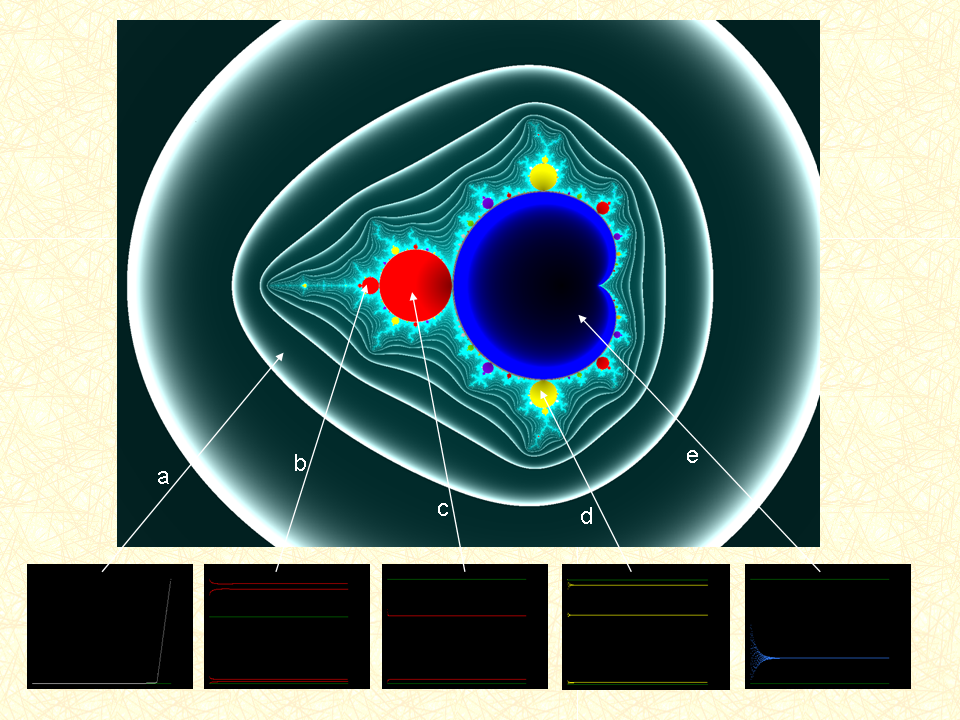
- arrow a in the image below: divergence - grey
- arrow b in the image below: oscillation with 4 points - red
- arrow c in the image below: oscillation with 2 points - red
- arrow d in the image below: oscillation with 3 points - yellow
- arrow e in the image below: fixpoint convergence with 1 fixpoint - blue
- the little black pictures at the bottom show the behaviour of the values |zi| for individual points c
- in the little black pictures at the bottom the green lines are reference lines with values 0.0 and 1.0, the white line shows divergence, the red and yellow ones oscillation, the blue line shows a fixpoint