Desert pictures are when f(z)=P1(z) / P2(z), with P1,P2 polynomials and degree(P1)≤degree(P2).
This results in more or less rough pictures with a brown surrounding in the standard rendering.
In the table scaled 0.8 is the scale value of the function: scale*f(z,c): 0.8*f(z,c).
In the table s=0.25 is the start value 0.25 of the iteration. Please see math basics.
In the table the link "scaling" is a link to show the scaled variants of f(z,c).
Clicking on the thumbnail image, a large version is shown.

scaled 1.0 s=0.01 scaling |

scaled 2.74 s=0.0 scaling |

scaled -10.0 s=-2.0 scaling |

scaled 200.0 s=4.0 scaling |

scaled 1.0 s=0.0 scaling |

scaled 1.0 s=1.0 scaling |
|
|
|
|
|
|
|
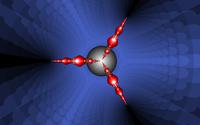
scaled 1.0 s=0.0 scaling |

scaled 1.0 s=0.0 scaling |

scaled 1.0 s=0.0 scaling |

scaled 1.0 s=1.0 scaling |

scaled -4.5 s=0.171573 scaling |

scaled 1.0 s=1.0 scaling |
|
|
|
|
|
|
|

scaled -2.4 s=1.0 scaling |

scaled 1.0 s=1.0 scaling |

scaled -15.7 s=-1.0 scaling |

scaled 28.2 s=1.0 scaling |

scaled 10.0 s=0.5 scaling |

scaled2.3 s=-1.259921 scaling |
|
|
|
|
|
|
|