What about f(z,c) = z*c + 1/z*c? Where z and c are intermixed with multiplication. Or what about f(z,c) = z^c or f(z,c) = c^z ?
In the table scaled 1.0 is the scale value of the function: scale*f(z,c): 1.0*f(z,c).
Scaling f(z,c) functions in general is not of much value.
In the table s=0.25 is the start value 0.25 of the iteration. Please see math basics.
In the table the link "powered" is a link to show the powered variants of f(z,c): f(z^2,c^3), f(z^n,c^m).
Clicking on the thumbnail image, a large version is shown.

scaled 1.0 s=0.0 powered |

scaled 1.0 s=0.0 powered |

scaled 1.0 s=0.0 powered |

scaled 1.0 s=2.0 powered |

scaled 1.0 s=3.330190676786 powered |

scaled 1.0 s=2.0 powered |
|
|
|
|
|
|
|

scaled 1.0 s=2.0 powered |

scaled 1.0 s=0.5 powered |
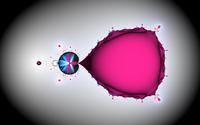
scaled 1.0 s=0.148148148 powered |
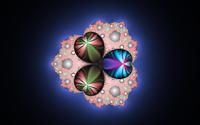
scaled 1.0 s=1.88988157 powered |

scaled 1.0 s=1.889881575 powered |

scaled 1.0 s=2.0 powered |
|
|
|
|
|
|
|

scaled 1.0 s=4.0 powered |

scaled 1.0 s=-4.0 powered |

scaled 1.0 s=-4.828427125 powered |

scaled 1.0 s=1.0 powered |

scaled 1.0 s=-0.472470394 powered |

scaled 1.0 s=0.300283106 powered |
|
|
|
|
|
|
|