Convergence to Perfect Apple Manikin Sets

What happens if one looks at the sequence of fractal images,
when you calculate fractal images changing the start value s?

For some values of s the fractal images converge to a Perfect Apple Manikin Set.

Mathematical Questions

Regarding this there are two mathematical questions I have.
I can only answer them by generating fractal images, not by calculating the answers.

  • 1) Given a function f(z,c) and a start value s, will this result in a Perfect Apple Manikin Set?
  • 2) Given a function f(z,c), what are the start values si, where the set converges to a Perfect Apple Manikin Set?

    • Update Eastern 2010: Answer to question 1): Calculate the number of Fractal Oscillation Circles.
    If this number is infinite, then it results in a Perfect Apple Manikin Set. See the definition page for an explanation.

    Convergence to Perfect Apple Manikin Sets
    mandelbrot set
    nova/ferguson nova sequence
    nova/ferguson nova
    nova sequence
    nova
    eight start values
    mandelbrot set animation
    mandelbrot set images
    double ferguson nova animation
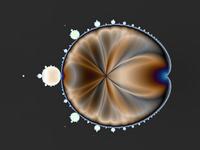
    two apple manikins animation

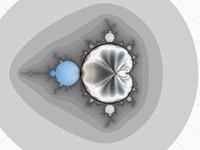
  • mandelbrot set: the mandelbrot set f(z) = z*z converges at s = 0.0, as already known.
  • nova/ferguson nova sequence: this nova/ferguson nova converges at s = -19.031269599284, 1.01563481 to a perfect nova, at s = -17.0, s = 0.0 to a ferguson nova, and at s = 0.510966297 to another nova. At s = 0.0 the fractal set is NaN (not a number, division by 0), but close to 0.0, e.g. at 0.00000000001, it is a perfect ferguson nova (well, almost, only very close)
  • nova/ferguson nova: showing the nova set at s = -19.031269599284, the ferguson nova at s = 0.000000000001, and the second nova at s = 0.510966297 in full size.
  • nova sequence: this nova converges at s = -0.064025469 to a nova and at 2.387861482 to another nova.
  • nova: showing the nova at s = -0.064025469 and the other nova at 2.387861482 in full size.
  • f(z,c) = ez - z5/(2 + 2z3 - 2z4)+c: this fractal set has eight start values, with four different fractal images:
    -1.0702392, -0.813785594, -0.7968692479, -0.5841301,0.9811992, 1.24616644591,1.269438192719 and 1.677332376
  • mandelbrot set animation: an animation showing a mandebrot set while changing the start value s.
  • mandelbrot set images: showing the single images of the mandelbrot set animation with start values:
    -0.020841442000, -0.078153273519, -0.4547833 and -0.818160797893. Two different images out of four.
    Additionally three zoom images are shown.
  • double ferguson nova animation: an animation showing a double ferguson nova set while changing the start value s.
  • two apple manikins animation: an animation showing two apple manikins while changing the start value s.